This is the first revision of the page. The external styles and javascript are gone (except MathJax), making it much faster to load (about 6 seconds).
Return to Speed up MathJax slow loading time
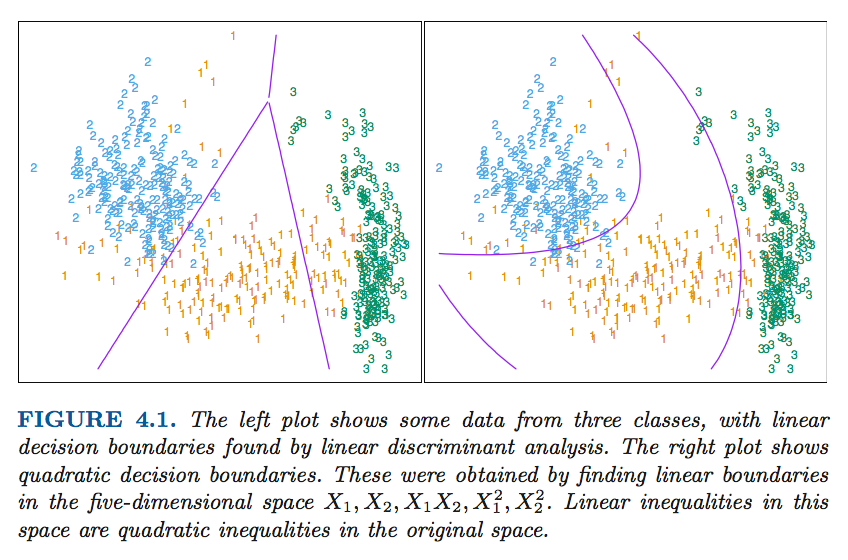
Since our predictor $G(x)$ takes values in a discrete set $\mathcal{G}$, we can always divide the input space into a collection of regions labeled according to the classification. We saw in Chapter 2 that the boundaries of these regions can be rough or smooth, depending on the prediction function. For an important class of procedures, these decision boundaries are linear; this is what we it mean by linear methodds for classification.
To build the connection between features $X$ and discrete outcomes, we could reply on logit transformation as follows:
\begin{align} \text{Pr}(G=1|X=x) &= \frac{\exp(\beta_0+\beta^Tx)}{1+\exp(\beta_0+\beta^Tx)},\\ \text{Pr}(G=2|X=x) &= \frac{1}{1+\exp(\beta_0+\beta^Tx)},\\ \end{align}where the monotone transformation is the logit transformation
$$ \log\frac{p}{1-p}, $$and in fact we see that
\begin{equation} \log\frac{\text{Pr}(G=1|X=x)}{\text{Pr}(G=2|X=x)} = \beta_0 + \beta^Tx. \end{equation}The decision boundary is the set of points for which the log-odds are zero, and this is a hyperplane defined by
$$ \left\lbrace x: \beta_0+\beta^Tx = 0 \right\rbrace. $$We will discuss two very popular but different methods that result in linear log-odds or logits: Linear discriminant analysis and linear logistic regression.
Once could also classify discrete outcomes without using log likelihood functions, which means we can explicitly model the boundaries between the classes as linear.
We will look at two methods that explicitly look for "separating hyperplanes".
When a separating hyperplane could be found we say it is linear classficiable, whereas we need to use neural network to classifiy them.

import math
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
%config InlineBackend.figure_formats = ['svg']
Here each of the response categories are coded via an indicator variable. For example,
$$Y_3 = [0, 0, 1, 0, 0]$$assuming we have 5 classes. This is also called one-hot encoding.
Thus if $\mathcal{G}$ has $K$ classes, there will be $K$ such indicators $Y_k$, $k=1,\cdots,K$, with
$$ Y_k = 1 \text{ if } G = k \text{ else } 0. $$These are collected together in a vector $Y=(Y_1,\cdots,Y_k)$, and the $N$ training instances of these form an $N\times K$ indicator response matrix $\mathbf{Y}$, which is a matrix of $0$'s and $1$'s, with each row having a single $1$.
For example,
$$ Y = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ & & \vdots & & \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} $$We fit a linear regression model to each of the columns of $\mathbf{Y}$ simultaneously, and the fit is given by
\begin{equation} \hat{\mathbf{Y}} = \mathbf{X}\left(\mathbf{X}^T\mathbf{X}\right)^{-1}\mathbf{X}^T\mathbf{Y} = \mathbf{X}\hat{\mathbf{B}}. \end{equation}Note that we have a coefficient vector for each response columns $\mathbf{y}_k$, and hence a $(p+1)\times K$ coefficient matrix $\hat{\mathbf{B}} = \left(\mathbf{X}^T\mathbf{X}\right)^{-1}\mathbf{X}^T\mathbf{Y}$. Here $\mathbf{X}$ is the model matrix with $p+1$ columns with a leading columns of $1$'s for the intercept.
A new observation with input $x$ is classified as follows:
There is a serious problem with the regression approach when the number of class $K\ge 3$, especially prevalent when $K$ is large. Because of the rigid nature of the regression model, classes can be masked by others. FIGURE 4.2 illustrates an extreme situation when $K=3$. The three classes are perfectly separated by linear decision boundaries, yet linear regression misses the middle class completely.
def generate_data(sample_size, feature_size, cluster_means, cluster_cov):
"""
sample size = n \\
feature size = m \\
classes are fixed = 3 or cluster = 3 ;
"""
# generate values for features x1 and x2
xx = np.random.multivariate_normal(
cluster_means, cluster_cov, size=(sample_size, feature_size)
).flatten(order='F').reshape(-1, feature_size)
# constant values
const = np.ones((sample_size*3, 1))
# stack all values
xmat = np.hstack(
[const, xx]
)
# generate labels
nplabel = np.repeat(
['c1', 'c2', 'c3'], sample_size).reshape(-1, 1)
column_names = ['const']
for i in range(feature_size):
temp = 'x'+str(i+1)
column_names.append(temp)
sdata = pd.DataFrame(
xmat,
columns=column_names
)
sdata['class'] = nplabel
ymat = pd.get_dummies(sdata['class'])
return sdata, xmat, ymat
# generate three clusters
np.random.seed(789)
sample_mean = [-4, 0, 4]
sample_cov = np.eye(3)
sdata, xmat, ymat = generate_data(300, 2, sample_mean, sample_cov)
sdata.head()
| const | x1 | x2 | class | |
|---|---|---|---|---|
| 0 | 1.0 | -5.108111 | -3.932767 | c1 |
| 1 | 1.0 | -4.425128 | -2.733287 | c1 |
| 2 | 1.0 | -2.815007 | -3.383044 | c1 |
| 3 | 1.0 | -1.927488 | -3.286930 | c1 |
| 4 | 1.0 | -2.506928 | -3.792087 | c1 |
# one hot encoding
ymat.head()
| c1 | c2 | c3 | |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 1 | 0 | 0 |
# fit linear regression
beta = np.linalg.solve(xmat.T @ xmat, xmat.T @ ymat)
beta
array([[ 0.33526599, 0.33314592, 0.33158809],
[-0.05184917, -0.00616798, 0.05801715],
[-0.06709384, 0.00617052, 0.06092332]]) def estimate_class(beta, xmat):
y_est = xmat @ beta
estimated_class = y_est.argmax(axis=1)+1
estimated_class = estimated_class.astype('str')
estimated_class = np.core.defchararray.add(
np.array(['c']*900), estimated_class
)
return y_est, estimated_class
# calculate estimation
y_est, estimated_class = estimate_class(beta, xmat)
y_est.shape
(900, 3)
So far, we have
Now, we will:
pd.Series(y_est.argmax(axis=1)).value_counts()
0 448 2 441 1 11 dtype: int64
Notice, that most of observations from class 2 are masked as either as class 1 or class 3. Now, we will plot the original dataset and estimated classes.
sdata['est_class'] = estimated_class
sdata.head()
| const | x1 | x2 | class | est_class | |
|---|---|---|---|---|---|
| 0 | 1.0 | -5.108111 | -3.932767 | c1 | c1 |
| 1 | 1.0 | -4.425128 | -2.733287 | c1 | c1 |
| 2 | 1.0 | -2.815007 | -3.383044 | c1 | c1 |
| 3 | 1.0 | -1.927488 | -3.286930 | c1 | c1 |
| 4 | 1.0 | -2.506928 | -3.792087 | c1 | c1 |
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
sns.scatterplot(x='x1', y='x2', hue='class',
data=sdata, ax=axes[0]);
axes[0].set_title("Original Dataset")
sns.scatterplot(x='x1', y='x2', hue='est_class',
data=sdata, ax=axes[1]);
axes[1].set_title("Estimated Class");
# add boundary line
xx1 = np.linspace(-7, 4)
y1 = -0.7*xx1-3.5
axes[0].plot(xx1, y1, 'k--');
xx2 = np.linspace(-3, 6)
y2 = -0.7*xx2+3
axes[0].plot(xx2, y2, 'k--');
y3 = -0.7*xx2
axes[1].plot(xx2, y3, 'k--');
The three classes are perfectly separated by linear decision boundaries, yet linear regression misses the middle class completely. Now, we will generate another dataset that each observation has only one feature $x_1$.
# figure 4.3 another example of masking class
# with one feature
np.random.seed(234)
sdata2, xmat2, ymat2 = generate_data(300, 1, sample_mean, sample_cov)
sdata2.head()
| const | x1 | class | |
|---|---|---|---|
| 0 | 1.0 | -3.181208 | c1 |
| 1 | 1.0 | -3.078422 | c1 |
| 2 | 1.0 | -4.969733 | c1 |
| 3 | 1.0 | -2.574784 | c1 |
| 4 | 1.0 | -5.283554 | c1 |
# linear regression with degree 1
beta_degree1 = np.linalg.solve(xmat2.T @ xmat2, xmat2.T @ ymat2)
beta_degree1
array([[ 3.33554011e-01, 3.33332814e-01, 3.33113175e-01],
[-1.12992566e-01, 2.65736676e-04, 1.12726830e-01]]) # fit with linear regression of degree 1 and degree 2
xmat2_sqr = np.hstack([xmat2, xmat2[:, 1:] * xmat2[:, 1:]])
beta_degree2 = np.linalg.solve(xmat2_sqr.T @ xmat2_sqr, xmat2_sqr.T @ ymat2)
beta_degree2
array([[ 0.12511596, 0.75642206, 0.11846198],
[-0.11246881, -0.0007974 , 0.1132662 ],
[ 0.01739609, -0.03531073, 0.01791463]]) y_est1, estimated1 = estimate_class(beta_degree1, xmat2)
sdata2['est_degree1'] = estimated1
y_est2, estimated2 = estimate_class(beta_degree2, xmat2_sqr)
sdata2['est_degree2'] = estimated2
sdata2.head()
| const | x1 | class | est_degree1 | est_degree2 | |
|---|---|---|---|---|---|
| 0 | 1.0 | -3.181208 | c1 | c1 | c1 |
| 1 | 1.0 | -3.078422 | c1 | c1 | c1 |
| 2 | 1.0 | -4.969733 | c1 | c1 | c1 |
| 3 | 1.0 | -2.574784 | c1 | c1 | c1 |
| 4 | 1.0 | -5.283554 | c1 | c1 | c1 |
pd.Series(y_est1.argmax(axis=1)).value_counts()
0 453 2 447 dtype: int64
pd.Series(y_est2.argmax(axis=1)).value_counts()
1 333 2 285 0 282 dtype: int64
We can see that the quadratic regression solve the masking issue.
# plot the results
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
sns.scatterplot(
x='x1', y=-0.5, hue='class', data=sdata2, ax=axes[0]
)
axes[0].plot(xmat2[:, 1], y_est1[:, 0],
color='#2678B2', linestyle='dashed')
axes[0].plot(xmat2[:, 1], y_est1[:, 1],
color='#FD7F28', linestyle='dashed')
axes[0].plot(xmat2[:, 1], y_est1[:, 2],
color='#339F34', linestyle='dashed')
axes[0].set_title('Degree = 1; Error = 0.33')
sns.scatterplot(
x='x1', y=-1, hue='class', data=sdata2, ax=axes[1]
)
axes[1].scatter(xmat2[:, 1], y_est2[:, 0],
color='#2678B2', s=2)
axes[1].scatter(xmat2[:, 1], y_est2[:, 1],
color='#FD7F28', s=2)
axes[1].scatter(xmat2[:, 1], y_est2[:, 2],
color='#339F34', s=2)
axes[1].set_title('Degree = 2; Error = 0.04');
# get predicted class
sdata2['y_pred1'] = np.max(y_est1, axis=1)
sdata2['y_pred2'] = np.max(y_est2, axis=1)
sdata2.head()
| const | x1 | class | est_degree1 | est_degree2 | y_pred1 | y_pred2 | |
|---|---|---|---|---|---|---|---|
| 0 | 1.0 | -3.181208 | c1 | c1 | c1 | 0.693007 | 0.658953 |
| 1 | 1.0 | -3.078422 | c1 | c1 | c1 | 0.681393 | 0.636200 |
| 2 | 1.0 | -4.969733 | c1 | c1 | c1 | 0.895097 | 1.113709 |
| 3 | 1.0 | -2.574784 | c1 | c1 | c1 | 0.624486 | 0.530027 |
| 4 | 1.0 | -5.283554 | c1 | c1 | c1 | 0.930556 | 1.204979 |
# now we plot the results again
# plot the results
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
sns.scatterplot(
x='x1', y=-0.5, hue='class', data=sdata2,
palette=['#2678B2', '#FD7F28', '#339F34'],
ax=axes[0]
)
sns.scatterplot(
x='x1', y='y_pred1', hue='est_degree1', data=sdata2,
legend=False,
palette=['#2678B2', '#339F34'],
ax=axes[0]
)
axes[0].set_title('Degree = 1; Error = 0.33')
axes[0].annotate('class 2 was masked completely',
(-4, -0.2));
sns.scatterplot(
x='x1', y=-1, hue='class', data=sdata2, ax=axes[1]
)
sns.scatterplot(
x='x1', y='y_pred2', hue='est_degree2', data=sdata2,
legend=False,
ax=axes[1]
)
axes[1].annotate('class 2 was not masked',
(-3.5, 1));
axes[1].set_title('Degree = 2; Error = 0.04');
For this simple example a quadratic rather than linear fit would solve the problem. However, if there were 4 classes, a quadratic would not come down fast enough, and a cubic would be needed as well. A loose but general rule is that if $K\ge 3$ classes are lined up, polynomial terms up to degree $K-1$ might be needed to resolve them.
Note also that these are polynomials along the derived direction passing through the centroids, which can have orbitrary orientation. So in $p$-dimensional input space, one would need general polynomial terms and cross-products of total degree $K-1$, $O(p^{K-1})$ terms in all, to resolve such worst-case scenarios.
The example is extreme, but for large $K$ and small $p$ such maskings naturally occur. As a more realistic illustration, FIGURE 4.4 is a projection of the training data for a vowel recognition problem onto an informative two-dimensional subspace.
# figure 4.4
vowel = pd.read_csv('./data/vowel/vowel.train', index_col=0)
vowel.head()
| y | x.1 | x.2 | x.3 | x.4 | x.5 | x.6 | x.7 | x.8 | x.9 | x.10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| row.names | |||||||||||
| 1 | 1 | -3.639 | 0.418 | -0.670 | 1.779 | -0.168 | 1.627 | -0.388 | 0.529 | -0.874 | -0.814 |
| 2 | 2 | -3.327 | 0.496 | -0.694 | 1.365 | -0.265 | 1.933 | -0.363 | 0.510 | -0.621 | -0.488 |
| 3 | 3 | -2.120 | 0.894 | -1.576 | 0.147 | -0.707 | 1.559 | -0.579 | 0.676 | -0.809 | -0.049 |
| 4 | 4 | -2.287 | 1.809 | -1.498 | 1.012 | -1.053 | 1.060 | -0.567 | 0.235 | -0.091 | -0.795 |
| 5 | 5 | -2.598 | 1.938 | -0.846 | 1.062 | -1.633 | 0.764 | 0.394 | -0.150 | 0.277 | -0.396 |
df_y = vowel['y']
df_x2d = vowel[['x.1', 'x.2']]
grouped = df_x2d.groupby(df_y)
fig, ax = plt.subplots(1, 1, figsize=(6, 4))
for y, x in grouped:
x_mean = x.mean() # mean of (x1 and x2) for each group
color = next(ax._get_lines.prop_cycler)['color']
ax.scatter(x['x.1'], x['x.2'],
edgecolor=color, facecolors='none')
ax.plot(x_mean[0], x_mean[1], 'o', color=color, markersize=10,
markeredgecolor='black', markeredgewidth=3)
ax.set_xlabel('Coordinate 1 for Training Data')
ax.set_ylabel('Coordinate 2 for Training Data')
ax.set_title('Linear Discriminant Analysis');
There are K = 11 classes in p = 10 dimensions. This is a difficult classification problem, and the best methods achieve around 40% errors on the test data. The main point here is summarized in Table 4.1; linear regression has an error rate of 67%, while a close relative, linear discriminant analysis, has an error rate of 56%. It seems that masking has hurt in this case. While all the other methods in this chapter are based on linear functions of x as well, they use them in such a way that avoids this masking problem.
| Technique | Error Rate | |
|---|---|---|
| Training | Test | |
| Linear regression | 0.48 | 0.67 |
| Linear discriminant analysis | 0.32 | 0.56 |
| Quadratic discriminant analysis | 0.01 | 0.53 |
| Logistic regression | 0.22 | 0.51 |
To summarize, there are at least two reasons not to perform classification using a regression method:
Decision theory for classification tells us that we need to know the class posteriors mass function $\text{Pr}(G|X)$ for optimal classification. Suppose
A simple application of Bayes theorem gives us
\begin{equation} \text{Pr}(G=k|X=x) = \frac{f_k(x)\pi_k}{\sum_{l=1}^K f_l(x)\pi_l}. \end{equation}We see that in terms of ability to classify, it is enough to have the $f_k(x)$. Many techniques are based on models for the class densities:
Suppose that we model each class density as multivariate Gaussian
\begin{equation} f_k(x) = \frac{1}{(2\pi)^{p/2}|\Sigma_k|^{1/2}}\exp\left\lbrace -\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k) \right\rbrace \end{equation}where $p$ is the number of feature dimension.
Linear discriminant analysis (LDA) arises in the special case when we assume that the classes have a common covariance matrix $\Sigma_k=\Sigma,\forall k$.
In comparing two classes $k$ and $l$, it is sufficient to look at the log-ratio, and we see that as an equation linear in $x$,
\begin{aligned} \log\frac{\text{Pr}(G=k|X=x)}{\text{Pr}(G=l|X=x)} &= \log\frac{f_k(x)}{f_l(x)} + \log\frac{\pi_k}{\pi_l} \\ &= \log\frac{\pi_k}{\pi_l} - \frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k + \frac{1}{2}\mu_l^T\Sigma^{-1}\mu_l + x^T\Sigma^{-1}(\mu_k-\mu_l) \\ &= \delta_k(x) - \delta_l(x), \end{aligned}where $\delta_k$ is the linear discriminant function
\begin{equation} \delta_k(x) = x^T\Sigma^{-1}\mu_k - \frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k + \log\pi_k. \end{equation}This linear log-odds function implies that the decision boundary between classes $k$ and $l$
\begin{equation} \left\lbrace x: \delta_k(x) - \delta_l(x) = 0 \right\rbrace \end{equation}is linear in $x$; in $p$ dimensions a hyperplane. Also the linear discriminant functions are equivalent description of the decision rule, with
\begin{equation} G(x) = \arg\max_k \delta_k(x). \end{equation}## why the decision boundary between classes k and l implies
## delta_k(x) - delta_l(x) = 0
## if the posterior pk > pl, then classified it as k
np.random.seed(889)
pk = np.random.uniform(0, 1, 100)
pl = np.random.uniform(0, 1, 100)
odds_ratio = pk/pl
cls_kl = np.where(odds_ratio > 1, 'class-k', 'class-l')
boundary_data = pd.DataFrame(
[pk, pl, odds_ratio, cls_kl]
)
boundary_data = boundary_data.transpose()
boundary_data.columns = ['pk', 'pl', 'odds_ratio', 'classification']
boundary_data.head()
| pk | pl | odds_ratio | classification | |
|---|---|---|---|---|
| 0 | 0.428559 | 0.444959 | 0.963144 | class-l |
| 1 | 0.807978 | 0.875746 | 0.922616 | class-l |
| 2 | 0.749596 | 0.364627 | 2.055786 | class-k |
| 3 | 0.405277 | 0.922467 | 0.43934 | class-l |
| 4 | 0.274735 | 0.40617 | 0.676402 | class-l |
fig, axes = plt.subplots(1, 1, figsize=(6, 4))
sns.scatterplot(
x='pl', y='pk', hue='classification',
data=boundary_data, ax=axes
)
xx = np.linspace(0, 1, 100)
axes.plot(xx, xx, 'k--');
The figure above shows why we set decision boundary between classes $k$ and $l$
\begin{equation} \left\lbrace x: \delta_k(x) - \delta_l(x) = 0 \right\rbrace \end{equation}as $log 1 = 0 $.
Note
For LDA, bayesian estimation and maximum likelihood estimation are equivament.
That's why we have the following decision rule too:
\begin{equation} G(x) = \arg\max_k \delta_k(x). \end{equation}# figure 4.5, a simulated example
np.random.seed(666)
sample_size = 30
sample_mean = [-0.5, 0, 0.5]
# generate a positive semidefinite matrix
rand_mat = np.random.rand(3, 3)
sample_cov = rand_mat.T @ rand_mat / 10
sdata3, xmat3, ymat3 = generate_data(
sample_size, 2, sample_mean, sample_cov
)
# now we will shift x2 down
sdata3['x2roll'] = np.roll(sdata3['x2'], 30)
sdata3.head()
| const | x1 | x2 | class | x2roll | |
|---|---|---|---|---|---|
| 0 | 1.0 | -0.071273 | -0.182977 | c1 | 0.466982 |
| 1 | 1.0 | -0.670211 | -0.320429 | c1 | 0.441147 |
| 2 | 1.0 | -0.800962 | -0.615667 | c1 | 0.274339 |
| 3 | 1.0 | -0.691924 | -0.543417 | c1 | 0.713403 |
| 4 | 1.0 | -0.598135 | -0.498490 | c1 | 0.492381 |
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
sns.kdeplot(
x='x1', y='x2', hue='class', alpha=0.5,
data=sdata3, ax=axes[0]
)
axes[0].set_title('Generated Data without rolling x2')
sns.move_legend(axes[0], 'upper left') # move legend
sns.kdeplot(
x='x1', y='x2roll', hue='class', alpha=0.5,
data=sdata3, ax=axes[1]
)
sns.scatterplot(
x='x1', y='x2roll', hue='class', data=sdata3, ax=axes[1]
)
axes[1].set_title('Generated Data with rolling x2');
Now, we will estimate the class via the linear discriminant functions:
$$ \delta_k(x) = x^T\Sigma^{-1}\mu_k - \frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k + \log\pi_k. $$In practice we do not know the parameters of the Gaussian distributions, and will need to estimate them using our training data:
## chose 80% of sdata3 as tranning dataset
training_data = sdata3.sample(frac=0.8)
# estimate prior, mean and variance
prior_hat = (training_data.groupby(
['class']
).count()/training_data.shape[0])['const']
prior_hat
class c1 0.361111 c2 0.305556 c3 0.333333 Name: const, dtype: float64
# estimate mean
mean_hat = training_data.groupby(
['class']
).mean()[['x1', 'x2roll']]
mean_hat
| x1 | x2roll | |
|---|---|---|
| class | ||
| c1 | -0.542296 | 0.518047 |
| c2 | 0.020427 | -0.556884 |
| c3 | 0.507638 | 0.013990 |
# calcluate covariance for each group
cov_each_group = training_data.groupby(
['class']
)[['x1', 'x2roll']].cov()
cov_each_group
| x1 | x2roll | ||
|---|---|---|---|
| class | |||
| c1 | x1 | 0.110910 | -0.009916 |
| x2roll | -0.009916 | 0.042135 | |
| c2 | x1 | 0.147984 | -0.025898 |
| x2roll | -0.025898 | 0.101976 | |
| c3 | x1 | 0.032246 | -0.016600 |
| x2roll | -0.016600 | 0.209065 |
# calculate the average covariance
cov_hat = (cov_each_group.loc['c1'] + cov_each_group.loc['c2'] +
cov_each_group.loc['c3'])/(training_data.shape[0]-3)
cov_hat
| x1 | x2roll | |
|---|---|---|
| x1 | 0.004219 | -0.000760 |
| x2roll | -0.000760 | 0.005118 |
With the following formula:
$$ \delta_k(x) = x^T\Sigma^{-1}\mu_k - \frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k + \log\pi_k. $$np.linalg.inv(cov_hat)
array([[243.50634645, 36.13821796],
[ 36.13821796, 200.73295574]]) prior_hat
class c1 0.361111 c2 0.305556 c3 0.333333 Name: const, dtype: float64
# calculate linear discriminant scores
# x.shape = 1x2, covariance is 2x2 mean_hat should be 2x1
print(
f"X shape: {xmat3[:, 1:].shape}",
f"Cov shape: {cov_hat.shape}",
f"Mean shape: {mean_hat.shape}",
sep='\n'
)
X shape: (90, 2) Cov shape: (2, 2) Mean shape: (3, 2)
def discriminant_score(x_feature_vector):
"""
In our case, feature dimension p=2, but class dimenion K=3 \\
x_feature_vector shape = 1 x 2 \\
cov_mat = 2 x 2 \\
mean_hat shape = 2 x 1
"""
cov_inv = np.linalg.inv(cov_hat)
mean_c1 = mean_hat.loc['c1'].values.reshape(2, 1)
mean_c2 = mean_hat.loc['c2'].values.reshape(2, 1)
mean_c3 = mean_hat.loc['c3'].values.reshape(2, 1)
c1 = (
x_feature_vector @ cov_inv @ mean_c1 -
1/2 * mean_c1.T @ cov_inv @ mean_c1 +
np.log(prior_hat['c1'])
)
c2 = (
x_feature_vector @ cov_inv @ mean_c2 -
1/2 * mean_c2.T @ cov_inv @ mean_c2 +
np.log(prior_hat['c2'])
)
c3 = (
x_feature_vector @ cov_inv @ mean_c3 -
1/2 * mean_c3.T @ cov_inv @ mean_c3 +
np.log(prior_hat['c3'])
)
return [c1[0], c2[0], c3[0]]
# extrat features
xmat_features = training_data[['x1', 'x2roll']]
xmat_features.head()
| x1 | x2roll | |
|---|---|---|
| 54 | 0.020254 | 0.020241 |
| 88 | 0.421421 | 0.381563 |
| 51 | 0.571343 | -0.797902 |
| 73 | 0.289732 | 0.936149 |
| 21 | -0.080530 | 0.400724 |
# test the discriminant function
discriminant_score(
xmat_features.iloc[1, :].values.reshape(1, 2)
) # indeed, it gives the high score for c1
[array([-69.16687308]), array([-80.70709791]), array([27.62736642])]
Now, we will classify our trainning dataset calculate the accuracy. Then we will use the test dataset to test linear discriminant classification.
# estimate the class
y_est = np.apply_along_axis(discriminant_score, 1, xmat_features)
estimated_class = y_est.argmax(axis=1)+1
estimated_class = estimated_class.astype('str')
estimated_class = np.core.defchararray.add(
np.array(['c']), estimated_class
)
estimated_class
training_data['estimated_class'] = estimated_class
training_data.head()
| const | x1 | x2 | class | x2roll | estimated_class | |
|---|---|---|---|---|---|---|
| 54 | 1.0 | 0.020254 | 0.475237 | c2 | 0.020241 | c3 |
| 88 | 1.0 | 0.421421 | 0.857843 | c3 | 0.381563 | c3 |
| 51 | 1.0 | 0.571343 | -0.334370 | c2 | -0.797902 | c2 |
| 73 | 1.0 | 0.289732 | 0.648200 | c3 | 0.936149 | c3 |
| 21 | 1.0 | -0.080530 | -0.797902 | c1 | 0.400724 | c1 |
# calculate accuracy
sum(
training_data['class'] == training_data['estimated_class']
) / training_data.shape[0]
0.875
# now we will plot the simulated dataset and estimated results
fig, axes = plt.subplots(1, 1, figsize=(6, 4))
sns.kdeplot(
x='x1', y='x2roll', hue='estimated_class', alpha=0.5,
levels=5,
data=training_data, ax=axes
)
sns.scatterplot(
x='x1', y='x2roll', hue='class',
data=training_data, ax=axes
)
sns.move_legend(axes, 'lower left')
axes.set_title('Simulated data with estimated contours');
training_data.head()
| const | x1 | x2 | class | x2roll | estimated_class | |
|---|---|---|---|---|---|---|
| 54 | 1.0 | 0.020254 | 0.475237 | c2 | 0.020241 | c3 |
| 88 | 1.0 | 0.421421 | 0.857843 | c3 | 0.381563 | c3 |
| 51 | 1.0 | 0.571343 | -0.334370 | c2 | -0.797902 | c2 |
| 73 | 1.0 | 0.289732 | 0.648200 | c3 | 0.936149 | c3 |
| 21 | 1.0 | -0.080530 | -0.797902 | c1 | 0.400724 | c1 |
Note
LDA is equiavlent to linear regression with two classes (K=2). However, when K > 3, LDA is not the same as linear regression of the class indicator matrix, and it avoids the masking problems.
When we assume the covariance is different for each class, then based on the following equation
$$ f_k(x) = \frac{1}{(2\pi)^{p/2}|\Sigma_k|^{1/2}}\exp\left\lbrace -\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k) \right\rbrace $$the convenient cancellations do not occur. We then get quadratic discriminant functions (QDA),
\begin{equation} \delta_k(x) = -\frac{1}{2}\log|\Sigma_k| -\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k) + \log\pi_k \end{equation}The decision boundary between each pair of classes $k$ and $l$ is described by a quadratic equation $\left\lbrace x: \delta_k(x) = \delta_l(x) \right\rbrace$.
The estimates for QDA are similar to those for LDA, except that separate covariance matrices must be estimated for each class. When p is large this can mean a dramatic increase in parameters. Since the decision boundaries are functions of the parameters of the densities, counting the number of parameters must be done with care. For LDA, it seems there are $(K − 1) × (p + 1)$ parameters. Likewise for QDA there will be $(K-1) \times \{p(p+3)/2+1\}$ parameters. Both LDA and QDA perform well on an amazingly large and diverse set of classification tasks.
For a problem with $K$ classes, we could only need $K-1$ discriminant functions by arbitrarily choosing one class to be the base class. Then, the total number of estimated parameters for LDA is $(K-1)(p+1)$. However, for QDA, for each class $K$
The total number of estimated parameters is $(K-1) \times \{p(p+3)/2+1\}$
Therefore, the number of parameters estimated in LDA increases linearly with p while that of QDA increases quadratically with p. We would expect QDA to have worse performance than LDA when the dimension p is large.
Both techniques are widely used, and entire books are devoted to LDA. It seems that whatever exotic tools are the rage of the day, we should always have available these two simple tools. The question arises why LDA and QDA have such a good track record. The reason is not likely to be that the data are approximately Gaussian, and in addition for LDA that the covariances are approximately equal. More likely a reason is that the data can only support simple decision boundaries such as linear or quadratic, and the estimates provided via the Gaussian models are stable. This is a bias variance tradeoff—we can put up with the bias of a linear decision boundary because it can be estimated with much lower variance than more exotic alternatives.
We can find a compromise between LDA and QDA by regularizing the individual class covariance matrices. Regularization means that we put a certain restriction on the estimated parameters. In this case, we require that individual covariance matrix shrinks toward a common pooled covariance matrix through a penalty parameter $\alpha$:
$$\hat{\Sigma}_k (\alpha) = \alpha \hat{\Sigma}_k + (1-\alpha) \hat{\Sigma}$$where $\hat{\Sigma}$ is the pooled covariance matrix as used in LDA. The pooled covariance matrix can also be regularized toward an identity matrix through a penalty parameter $\gamma$
$$\hat{\Sigma} (\gamma) = \gamma \hat{\Sigma} + (1-\gamma) \sigma^2 I$$In situations where the number of input variables greatly exceeds the number of samples ($p>N$), the covariance matrix can be poorly estimated. Shrinkage can hopefully improve estimation and classification accuracy.
class DiscriminantAnalysis():
"""
Class for implimenting Regularized Discriminent Analysis
LDA is performed when alpha=0
QDA is performed when alpha=1
Linear, Quadratic and Regularized discriminant analysis.
Regularized discriminant analysis is a compromise between
linear discrimenent analysis and quadratic discrimenent analysis.
If you wish to add the constraint that the covariance matrix be
diagonal (independent features), use Naive Bayes instead.
Reference: https://github.com/christopherjenness/ML-lib
"""
def __init__(self, alpha=1.0) -> None:
self.is_model_fitted = False
self.alpha = alpha
self.class_categories = []
self.class_priors = {}
self.class_means = {}
self.regularized_covariances = {}
def fit(self, X, y):
"""
X: N by p matrix
y: N by 1 matrix
"""
# get unique classes
self.class_categories = np.unique(y)
# initialize the covariance
class_k_covs = {}
pooled_covs = 0
# estimate parameters: mean, covariance matrix and priors
for k in self.class_categories:
class_k_idx = np.where(y==k)[0]
class_k_features = X[class_k_idx, :]
self.class_priors[k] = float(len(class_k_idx)) / y.shape[0]
self.class_means[k] = np.mean(class_k_features, axis=0)
# each column as a variable
class_k_covs[k] = np.cov(class_k_features, rowvar=False)
# calculate pooled covariance
# alternative formula: pooled_covs += class_k_covs[k]
# pooled_covs = pooled_covs / (N-K)
pooled_covs += class_k_covs[k] * self.class_priors[k]
# calculate regularized covariance matrices for each class
# when alpha = 1, it is LDA, pooled covs is not used
for k in self.class_categories:
self.regularized_covariances[k] = (
self.alpha * class_k_covs[k] +
(1-self.alpha) * pooled_covs
)
self.is_model_fitted = True
def predict(self, X):
"""
X: sample size by p matrix [sample_size, p]
return: the predicted class [sample_size, 1] matrix
"""
y_est = np.apply_along_axis(
self.__classify, 1, X
)
return y_est
def __classify(self, x):
"""
Private method
x: feature vector for one observation [1, p] dimension
Returns: classified category
"""
if not self.is_model_fitted:
raise NameError('Please fit the model first')
# calculate the determinant score
classified_scores = {}
for k in self.class_categories:
mean_deviation = x-self.class_means[k]
# pinv is preferred becuase of erros of float (sigularity)
cov_inv = np.linalg.pinv(self.regularized_covariances[k])
# use the formula in the equation (1)
# for score1, we do not use np.log() as it might have 0s
score1 = -0.5 * np.linalg.det(
self.regularized_covariances[k]
)
score2 = -0.5 * mean_deviation.T @ cov_inv @ mean_deviation
score3 = np.log(self.class_priors[k])
classified_scores[k] = score1 + score2 + score3
# foo = {'a': 1, 'b': 3000, 'c': 0}
# print(max(foo, key=foo.get))
return max(classified_scores, key=classified_scores.get)
# figure 4.7
# read vowel train
vowel = pd.read_csv('./data/vowel/vowel.train', index_col=0)
vowel.head()
| y | x.1 | x.2 | x.3 | x.4 | x.5 | x.6 | x.7 | x.8 | x.9 | x.10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| row.names | |||||||||||
| 1 | 1 | -3.639 | 0.418 | -0.670 | 1.779 | -0.168 | 1.627 | -0.388 | 0.529 | -0.874 | -0.814 |
| 2 | 2 | -3.327 | 0.496 | -0.694 | 1.365 | -0.265 | 1.933 | -0.363 | 0.510 | -0.621 | -0.488 |
| 3 | 3 | -2.120 | 0.894 | -1.576 | 0.147 | -0.707 | 1.559 | -0.579 | 0.676 | -0.809 | -0.049 |
| 4 | 4 | -2.287 | 1.809 | -1.498 | 1.012 | -1.053 | 1.060 | -0.567 | 0.235 | -0.091 | -0.795 |
| 5 | 5 | -2.598 | 1.938 | -0.846 | 1.062 | -1.633 | 0.764 | 0.394 | -0.150 | 0.277 | -0.396 |
# read vowel test
vowel_test = pd.read_csv('./data/vowel/vowel.test', index_col=0)
vowel_test.head()
| y | x.1 | x.2 | x.3 | x.4 | x.5 | x.6 | x.7 | x.8 | x.9 | x.10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| row.names | |||||||||||
| 1 | 1 | -1.149 | -0.904 | -1.988 | 0.739 | -0.060 | 1.206 | 0.864 | 1.196 | -0.300 | -0.467 |
| 2 | 2 | -2.613 | -0.092 | -0.540 | 0.484 | 0.389 | 1.741 | 0.198 | 0.257 | -0.375 | -0.604 |
| 3 | 3 | -2.505 | 0.632 | -0.593 | 0.304 | 0.496 | 0.824 | -0.162 | 0.181 | -0.363 | -0.764 |
| 4 | 4 | -1.768 | 1.769 | -1.142 | -0.739 | -0.086 | 0.120 | -0.230 | 0.217 | -0.009 | -0.279 |
| 5 | 5 | -2.671 | 3.155 | -0.514 | 0.133 | -0.964 | 0.234 | -0.071 | 1.192 | 0.254 | -0.471 |
alpha_values = np.linspace(0, 1, 50)
train_mis_rate = []
test_mis_rate = []
# construct x and y
vowel_X = vowel.iloc[:, 1:].values
vowel_y = vowel.iloc[:, 0].values.reshape(-1, 1)
vowel_test_X = vowel_test.iloc[:, 1:].values
for alpha in alpha_values:
vowel_rda = DiscriminantAnalysis(alpha)
vowel_rda.fit(vowel_X, vowel_y)
y_pred = vowel_rda.predict(vowel_X)
# accuracy rate
acc_rate = sum(vowel['y'] == y_pred) / vowel.shape[0]
train_mis_rate.append(1-acc_rate)
y_pred = vowel_rda.predict(vowel_test_X)
acc_rate = sum(vowel_test['y'] == y_pred) / vowel_test.shape[0]
test_mis_rate.append(1-acc_rate)
# figure 4.7
fig, axes = plt.subplots(1, 1, figsize=(6, 4))
axes.scatter(
alpha_values, train_mis_rate,
color='#5BB5E7', s=7, label='Train Data'
)
axes.scatter(
alpha_values, test_mis_rate,
color='#E49E25', s=7, label='Test Data'
)
axes.set_title("Regularized Discriminant Analysis on the Vowel Data")
axes.set_ylabel("Misclassification Rate")
axes.set_xlabel(r"$\alpha$")
axes.legend();
Figure 4.7 shows the results of RDA applied to the vowel data. Both the training and test error improve with increasing $\alpha$, although the test error increases sharply after $\alpha = 0.9$. The large discrepancy between the training and test error is partly due to the fact that there are many repeat measurements on a small number of individuals, different in the training and test set.
In situations where the number of input variables greatly exceeds the number of samples ($p > N$), the covariance matrix can be poorly estimated. Shrinkage can hopefully improve estimation and classification accuracy. This is illustrated by the figure below.
def generate_data(n_samples, n_features):
"""
Generate random blob-ish data with noisy features.
K = 2, p = n_features
Only one feature contains discriminative information
The other features contain only noise.
"""
X, y = make_blobs(n_samples=n_samples, n_features=1, centers=[[-2], [2]])
# add non-discriminative features
if n_features > 1:
X = np.hstack([X, np.random.randn(n_samples, n_features - 1)])
return X, y
n_train = 20 # samples for training
n_test = 200 # samples for testing
n_simulation = 30 # number of simulation
n_features_max = 75 # maximum number of features
step = 4 # step size for the calculation
acc_clf1, acc_clf2 = [], []
n_features_range = range(1, n_features_max + 1, step)
for n_features in n_features_range:
# run simulation
score_clf1, score_clf2 = 0, 0
for _ in range(n_simulation):
X, y = generate_data(n_train, n_features)
# train the model, with alpha=0.5 and 0 (LDA)
clf1 = LinearDiscriminantAnalysis(solver='lsqr', shrinkage=0.5).fit(X, y)
clf2 = LinearDiscriminantAnalysis(solver='lsqr', shrinkage=None).fit(X, y)
X, y = generate_data(n_test, n_features)
score_clf1 += clf1.score(X, y)
score_clf2 += clf2.score(X, y)
# calculate average of simulations
acc_clf1.append(score_clf1 / n_simulation)
acc_clf2.append(score_clf2 / n_simulation)
features_samples_ratio = np.array(n_features_range) / n_train
fig, axes = plt.subplots(1, 1, figsize=(6, 4))
axes.plot(features_samples_ratio, acc_clf1, linewidth=1.5,
label="LDA with shrinkage", color='#282A3A')
axes.plot(features_samples_ratio, acc_clf2, linewidth=1.5,
label="LDA", color='#FD7F28')
axes.set_xlabel('n_features / n_samples')
axes.set_ylabel('Classification accuracy')
axes.legend(prop={'size': 9});
Tips
As a lead-in to the next topic, we briefly digress on the computations required for LDA and especially QDA. Their computations are simplified by diagonalizing $\hat{\mathbf{\Sigma}}$ or $\hat{\boldsymbol{\Sigma}}_k$. For the latter, suppose we compute the eigendecomposition for each $\hat{\boldsymbol{\Sigma}}_k=\mathbf{U}_k \mathbf{D}_k \mathbf{U}_k^T$, where $\mathbf{U}_k$ is $p \times p$ orthonormal, and $\mathbf{D}_k$ a diagonal matrix of positive eigenvalues $d_{k \ell}$. Then the ingredients for $\delta_k(x)(4.12)$ are
In light of the computational steps outlined above, the LDA classifier can be implemented by the following pair of steps:
When $p > K$, we do not have to feed in all dimensions of features as we just need input space lie in an affine subspace $\leq K-1$, and if $p$ is much larger than $K$, this will be a considerable drop in dimension. Moreover, in locating the closest centroid, we can ignore distances orthogonal to this subspace, since they will contribute equally to each class. Thus we might just as well project the $X^*$ onto this centroid-spanning subspace $H_{K-1}$, and make distance comparisons there.
Therefore there is a fundamental dimension reduction in LDA, namely, that we need only consider the data in a subspace of dimension at most $K-1$. If $K=3$, e.g., this could allow us to view the data in $\mathbb{R}^2$, color-coding the classes. In doing so we would not have relinquished any of the information needed for LDA classification.
Before we go through the algorithms, let's examine an example. For a wine classification problem with three different types of wines and 13 input variables, the plot visualizes the data in two discriminant coordinates found by LDA. In this two-dimensional space, the classes can be well-separated. In comparison, the classes are not as clearly separated using the first two principal components found by PCA.
from sklearn import datasets # import the dataset
from sklearn.decomposition import PCA
wine = datasets.load_wine()
X = wine.data
y = wine.target
target_names = wine.target_names
X_r_lda = LinearDiscriminantAnalysis(
n_components=2
).fit(X, y).transform(X)
X_r_pca = PCA(n_components=2).fit(X).transform(X)
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
for i, target_name in zip([0, 1, 2], target_names):
sns.scatterplot(
x=X_r_lda[y == i, 0], y=X_r_lda[y == i, 1],
label=target_name,
alpha=0.7, ax=axes[0]
)
sns.scatterplot(
x=X_r_pca[y == i, 0], y=X_r_pca[y == i, 1],
label=target_name,
alpha=0.7, ax=axes[1]
)
sns.move_legend(axes[0], 'lower right')
axes[0].set_title('LDA for Wine dataset')
axes[1].set_title('PCA for Wine dataset')
axes[0].set_xlabel('Discriminant Coordinate 1')
axes[0].set_ylabel('Discriminant Coordinate 2')
axes[1].set_xlabel('PC 1')
axes[1].set_ylabel('PC 2');
Tips
We have observed from the previous section that LDA makes distance comparison in the space spanned by different class means. Two distinct points lie on a 1d line; three distinct points lie on a 2d plane.
For the data with $K$ classes, all means lie on a hyperplane with dimension at most $(K-1)$. In particular, the subspace spanned by the means is
$$H_{K-1} = \mu_1 \bigoplus \text{span}\{\mu_i - \mu_1, 2 \leq i \leq K\}$$When making distance comparison in this space, distances orthogonal to this subspace would add no information since they contribute equally for each class. Hence, by restricting distance comparisons to this subspace only would not lose any information useful for LDA classification.
That means, we can safely transform our task from a $p$-dimensional problem to a $(K-1)$-dimensional problem by an orthogonal projection of the data onto this subspace.
How could we find the optimal subspace then? Fisher defined optimal to mean that the projected centroids were spread out as much as possible in terms of variance. This means we cover more data in this optimal subspace and used the maximum information we have:
In summary then, finding the sequences of optimal subspaces for LDA involves the following steps ($\hat{\mu}_k$ is a column vector denoting the mean vector of class $k$):
where
$$\hat{\mu}^* = \sum_{k=1}^K \pi_k \hat{\mu}_k = \text{sample mean}$$PCA: obtain L eigenvectors $v_l^*$ in $V^*$ of $B^* = V^*D_B V^{*T}$ corresponding to the $L$ largest eigenvalues. These define the coordinates of the optimal subspace.
Obtain $L$ new (discriminant) variables $Z_l = (W^{-1/2} v_l^*)^TX, for $l = 1, \cdots, L$
Through this procedure, we reduce our data from $X_{(N \times p)}$ to $Z_{(N \times L)}$ and dimension from $p$ to $L$. Discriminant coordinate 1 and 2 in the previous wine plot are found by setting $L=2$. Repeating the previous LDA procedures for classification using the new data, $Z$, is called the reduced-rank LDA.
Fisher does not make any assumptions about the distribution of the data. Instead, he tries to find a “sensible” rule so that the classification task becomes easier. In particular, Fisher finds a linear combination of the original data, $Z=a^TX$, where the between-class variance, $B=cov(M)$, is maximized relative to the within-class variance, $W$.
The following figure shows why this rule makes intuitive sense. The rule sets out to find a direction, $a$, where, after projecting the data onto that direction, class means have maximum separation between them, and each class has minimum variance within them. The projection direction found under this rule, shown in the right plot, makes classification much easier.
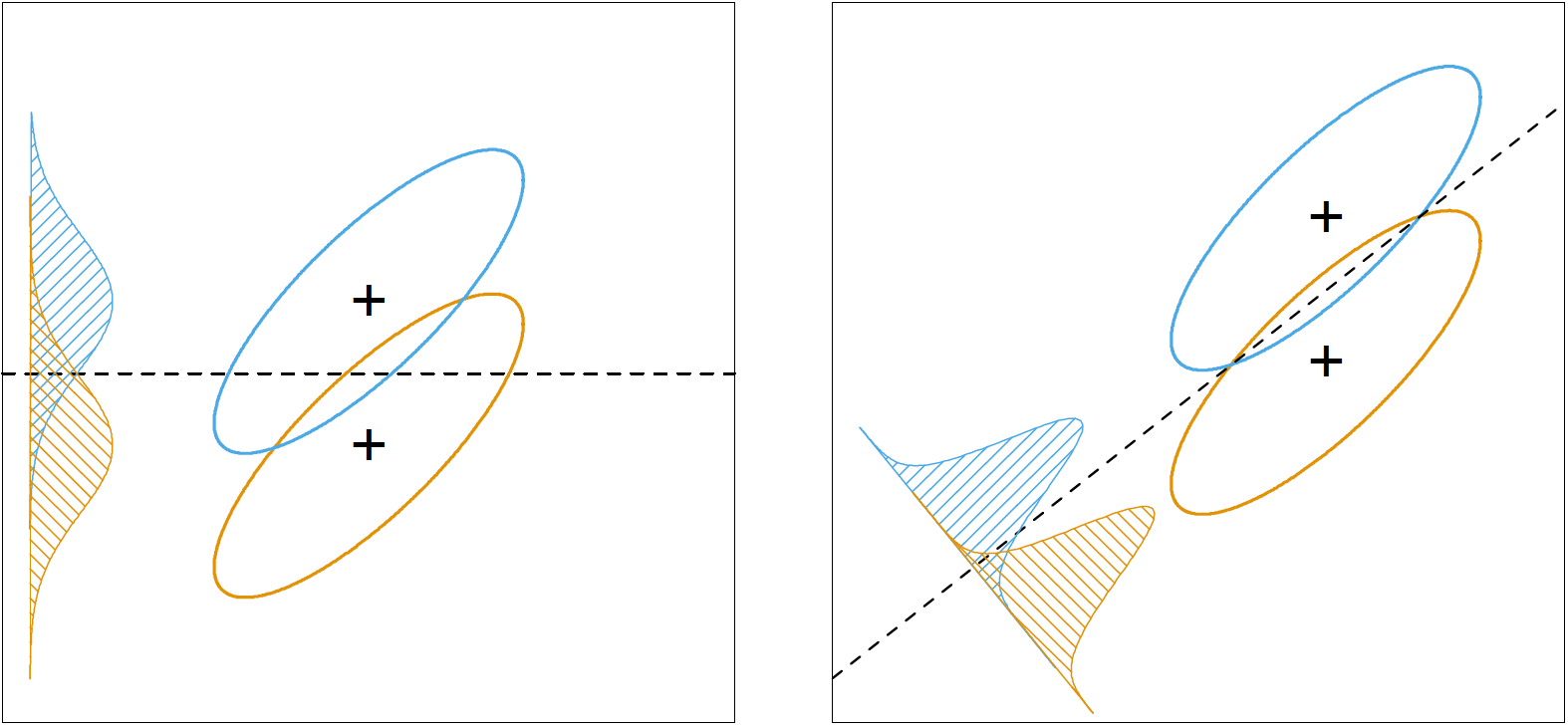
Fisher constructs two numbers:
\begin{aligned} R \ni d_B & := \mathbf{a}^T \mathbf{B a} \\ R \ni d_W & := \mathbf{a}^T \mathbf{W a} \end{aligned}He wants to maximize $d_B$ (spread-out) and minimize $d_W$ (cluster within class). We can merge those two optimization problems as a regularized optimization problem:
$$\max_a = d_B(a) - d_W(a) $$or : $$ \max _{\mathbf{a}} \frac{\mathbf{a}^T \mathbf{B a}}{\mathbf{a}^T \mathbf{W a}} . $$
The problem is equivalent to (see proof) $$ \begin{aligned} &\max _{\mathbf{a}} \mathbf{a}^T \mathbf{B a} \\ &\text { s.t. } \mathbf{a}^T \mathbf{W} \mathbf{a}=1 \end{aligned} $$ since the scaling of a does not affect the solution. Now, we could form the Lagrangian as
$$L = a^T B a - \lambda (a^T W a - 1)$$The solution is
$$Ba = \lambda W a \implies W^{-1}B a = \lambda a$$which is the eigenvalue and eigenvector problem and $a$ is the eigenvector of $W^{-1}B$. Because $W$ might be singular and not invertible, we will stretch the diagonal of $W$ slightly to make it full rank and invertible:
$$a = \text{eig} [(W+\epsilon I)^{-1} B] $$where $a$ is referred to as the Fisher direction or Fisher axis.
To summarize the developments so far:
Gaussian classification with common covariances leads to linear decision boundaries. Classification can be achieved by sphering the data with respect to $W$, and classifying to the closest centroid (modulo $\log \pi k$) in the sphered space.
Since only the relative distances to the centroids count, one can confine the data to the subspace spanned by the centroids in the sphered space.
This subspace can be further decomposed into successively optimal subspaces in term of centroid separation. This decomposition is identical to the decomposition due to Fisher
Once we transferred our dataset, we could classify according to the class $j = 1, \cdots, K$ for which
$$\frac{1}{2} || \tilde{x} - \tilde{\mu} ||^2 - \log \hat{\pi}_j$$is smalles, where $\tilde{x} = Ax \in R^{K-1}$ and $\tilde{\mu} = A \hat{\mu}_j$
class FDA:
"""
Fisher Discriminant Analysis
"""
def __init__(self, n_components=None, kernel=None):
"""
n_components: the number of components (or coordinates)
kernel: kernel of X
"""
self.is_model_fitted = False
self.n_components = n_components
# projection matrix
self.proj_matrix = None
self.class_categories = []
self.class_priors = {}
self.class_means = {}
if kernel is not None:
self.kernel = kernel
else:
self.kernel = 'linear'
def fit(self, X, y):
"""
X: N by p matrix
y: N by 1 matrix
"""
# get the unique classes
self.class_categories = np.unique(y)
# feature dimension
p = X.shape[1]
N = X.shape[0]
K = len(self.class_categories)
# estimate sample mean
sample_mean = X.mean(axis=0).reshape(p, 1)
# estimate between class covariance
# between scatter matrix B or S, p by p
B = np.zeros((p, p))
for k in self.class_categories:
class_k_row_idx = np.where(y==k)[0]
n_k = len(class_k_row_idx)
X_filtered_class_k = X[class_k_row_idx, :]
self.class_priors[k] = float(n_k)/N
self.class_means[k] = np.mean(
X_filtered_class_k, axis=0
).reshape(p, 1)
between_mean_diff = self.class_means[k] - sample_mean
# calculate B
# some people use weighted one
# n_k = len(class_k_row_idx)
# B += n_k * between_mean_diff @ between_mean_diff.T
B += between_mean_diff @ between_mean_diff.T
# estimate pooled covariance W
class_k_covs = {}
W = 0
for k in self.class_categories:
class_k_row_idx = np.where(y==k)[0]
X_filtered_class_k = X[class_k_row_idx, :]
# each column as a variable
class_k_covs[k] = np.cov(X_filtered_class_k, rowvar=False)
# calculate pooled covariance
W += class_k_covs[k] * self.class_priors[k]
# rank the eigenvalues
epsilon = 0.00001
# do not use eigh, it gives wrong eigenvectors
eig_val, eig_vec = np.linalg.eig(
np.linalg.pinv(W+epsilon*np.eye(W.shape[0])) @ B
)
# only take real values
eig_val = eig_val.real
eig_vec = eig_vec.real
# sort eigenvalues in descending order
eig_idx = eig_val.argsort()[::-1]
eig_val = eig_val[eig_idx]
eig_vec = eig_vec[:, eig_idx]
# get the coordinate matrix
if self.n_components is not None:
U = eig_vec[:, :self.n_components]
else:
U = eig_vec[:, :K-1]
self.proj_matrix = U
self.is_model_fitted = True
def transform(self, X):
"""
X: N by p matrix
projection matrix is p by K-1
"""
if not self.is_model_fitted:
raise NameError('Please fit the model first')
return X @ self.proj_matrix
def predict(self, X_transformed):
"""
X_transformed: sample size by p matrix [N, n_components <= K-1]
return: the predicted class [N, 1] matrix
"""
y_est = np.apply_along_axis(
self.__classify, 1, X_transformed
)
return y_est
def __classify(self, x_transformed):
"""
Private method
x_transformed:
feature vector for one observation [1, K-1] dimension
Returns: classified category
"""
if not self.is_model_fitted:
raise NameError('Please fit the model first')
# calculate the determinant score
classified_scores = {}
for k in self.class_categories:
# transform the mean, y by p - p by k-1
transformed_mean = self.class_means[k].T @ self.proj_matrix
mean_distance = np.linalg.norm(
x_transformed - transformed_mean
)
prior_hat = self.class_priors[k]
score = 0.5*np.square(mean_distance)-np.log(prior_hat)
classified_scores[k] = score
# !Warning: we want the minimal score now
return min(classified_scores, key=classified_scores.get)
# test the FDA
from sklearn import datasets # import the dataset
from sklearn.decomposition import PCA
wine = datasets.load_wine()
X = wine.data
y = wine.target
target_names = wine.target_names
# reduced dimension
wine_fda = FDA(n_components=2)
wine_fda.fit(X, y)
X_r_fda = wine_fda.transform(X)
X_r_pca = PCA(n_components=2).fit(X).transform(X)
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
for i, target_name in zip([0, 1, 2], target_names):
sns.scatterplot(
x=X_r_fda[y == i, 0], y=X_r_fda[y == i, 1],
label=target_name,
alpha=0.7, ax=axes[0]
)
sns.scatterplot(
x=X_r_pca[y == i, 0], y=X_r_pca[y == i, 1],
label=target_name,
alpha=0.7, ax=axes[1]
)
sns.move_legend(axes[0], 'lower right')
axes[0].set_title('FDA for Wine dataset')
axes[1].set_title('PCA for Wine dataset')
axes[0].set_xlabel('Discriminant Coordinate 1')
axes[0].set_ylabel('Discriminant Coordinate 2')
axes[1].set_xlabel('PC 1')
axes[1].set_ylabel('PC 2');
# figure 4.10
dimension = range(1, 11)
train_mis_rate = []
test_mis_rate = []
# construct x and y
vowel_X = vowel.iloc[:, 1:].values
vowel_y = vowel.iloc[:, 0].values.reshape(-1, 1)
vowel_test_X = vowel_test.iloc[:, 1:].values
for d in dimension:
vowel_fda = FDA(n_components=d)
vowel_fda.fit(vowel_X, vowel_y)
vowel_X_transformed = vowel_fda.transform(vowel_X)
y_pred = vowel_fda.predict(vowel_X_transformed)
# accuracy rate
acc_rate = sum(vowel['y'] == y_pred) / vowel.shape[0]
train_mis_rate.append(1-acc_rate)
vowel_test_X_transformed = vowel_fda.transform(vowel_test_X)
y_pred = vowel_fda.predict(vowel_test_X_transformed)
acc_rate = sum(vowel_test['y'] == y_pred) / vowel_test.shape[0]
test_mis_rate.append(1-acc_rate)
# figure 4.10
fig, axes = plt.subplots(1, 1, figsize=(6, 4))
axes.plot(
dimension, test_mis_rate,
color='#E49E25', linestyle='--', marker='o',
markersize=4, dashes=(17, 5),
label='Test Data'
)
axes.plot(
dimension, train_mis_rate,
color='#5BB5E7', linestyle='--', marker='o',
markersize=4, dashes=(25, 5),
label='Train Data'
)
axes.set_title("LDA and Dimension Reduction on the Vowel Data")
axes.set_ylabel("Misclassification Rate")
axes.set_xlabel("Dimension")
axes.legend();
import matplotlib.pyplot as plt
from sklearn import datasets, svm, metrics
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
digits = datasets.load_digits()
images_and_labels = list(zip(digits.images, digits.target))
for index, (image, label) in enumerate(images_and_labels[:4]):
plt.subplot(2, 4, index + 1)
plt.axis('off')
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
plt.title('Training: %i' % label)
plt.tight_layout()
X = digits.data
n_samples = X.shape[0]
y = digits.target
target_names = digits.target_names
# Create a classifier: a Fisher's LDA classifier
lda = LinearDiscriminantAnalysis(
n_components=4, solver='eigen', shrinkage=0.1
)
# Train lda on the first half of the digits
lda = lda.fit(X[:n_samples // 2], y[:n_samples // 2])
X_r_lda = lda.transform(X)
# Visualize transformed data on learnt discriminant coordinates
with plt.style.context('seaborn-talk'):
fig, axes = plt.subplots(1,2,figsize=[10,5])
for i, target_name in zip([0,1,2,3,4,5,6,7,8,9], target_names):
axes[0].scatter(
X_r_lda[y == i, 0], X_r_lda[y == i, 1],
alpha=.8, label=target_name,
marker='$%.f$'%i)
axes[1].scatter(
X_r_lda[y == i, 2], X_r_lda[y == i, 3],
alpha=.8, label=target_name,
marker='$%.f$'%i)
axes[0].set_xlabel('Discriminant Coordinate 1')
axes[0].set_ylabel('Discriminant Coordinate 2')
axes[1].set_xlabel('Discriminant Coordinate 3')
axes[1].set_ylabel('Discriminant Coordinate 4')
plt.tight_layout()
The above plot allows us to interpret the trained LDA classifier. For example, coordinate 1 helps to contrast 4’s and 2/3’s while coordinate 2 contrasts 0’s and 1’s. Subsequently, coordinate 3 and 4 help to discriminate digits not well-separated in coordinate 1 and 2. We test the trained classifier using the other half of the dataset. The report below summarizes the result.
n_samples = len(X)
# Predict the value of the digit on the second half:
expected = y[n_samples // 2:]
predicted = lda.predict(X[n_samples // 2:])
report = metrics.classification_report(expected, predicted)
print("Classification report:\n%s" % (report))
Classification report:
precision recall f1-score support
0 0.96 0.98 0.97 88
1 0.94 0.88 0.91 91
2 0.97 0.90 0.93 86
3 0.91 0.95 0.92 91
4 1.00 0.91 0.95 92
5 0.93 0.96 0.94 91
6 0.97 0.99 0.98 91
7 0.98 0.97 0.97 89
8 0.91 0.85 0.88 88
9 0.79 0.93 0.86 92
accuracy 0.93 899
macro avg 0.94 0.93 0.93 899
weighted avg 0.93 0.93 0.93 899
The highest precision is 99%, and the lowest is 77%, a decent result knowing that the method was proposed some 70 years ago. Besides, we have not done anything to make the procedure better for this specific problem. For example, there is collinearity in the input variables, and the shrinkage parameter might not be optimal.
The logistic regression model arises from the desire to model the posterior probabilities of the $K$ classes via linear functions in $x$, ensuring the natural properties of the probability: They sum to one and remain in $[0,1]$.
The model has the form
\begin{aligned} \log\frac{\text{Pr}(G=1|X=x)}{\text{Pr}(G=K|X=x)} &= \beta_{10} + \beta_1^Tx \\ \log\frac{\text{Pr}(G=2|X=x)}{\text{Pr}(G=K|X=x)} &= \beta_{20} + \beta_2^Tx \\ &\vdots \\ \log\frac{\text{Pr}(G=K-1|X=x)}{\text{Pr}(G=K|X=x)} &= \beta_{(K-1)0} + \beta_{K-1}^Tx \\ \end{aligned}The model is specified in terms of $K-1$ log-odds or logit transformations, reflecting the constraint that the probabilities sum to one. The choice of denominator ($K$ in this case) is arbitrary in that the estimates are equivalent under this choice.
To emphasize the dependence on the entire parameter set $\theta = \left\lbrace \beta_{10}, \beta_1^T, \cdots, \beta_{(K-1)0}, \beta_{K-1}^T\right\rbrace$, we denote the probabilities
\begin{equation} \text{Pr}(G=k|X=x) = p_k(x;\theta) \end{equation}A simple calculation shows that
\begin{aligned} \text{Pr}(G=k|X=x) &= \frac{\exp(\beta_{k0}+\beta_k^Tx)}{1+\sum_{l=1}^{K-1}\exp(\beta_{l0}+\beta_l^Tx)}, \text{ for } k=1,\cdots,K-1, \\ \text{Pr}(G=K|X=x) &= \frac{1}{1+\sum_{l=1}^{K-1}\exp(\beta_{l0}+\beta_l^Tx)}, \end{aligned}It is better to write it as the following form:
\begin{aligned} \text{Pr}(G=k|X=x) &= \frac{\exp(\beta_{k0}+\beta_k^Tx)}{\exp(0)+\sum_{l=1}^{K-1}\exp(\beta_{l0}+\beta_l^Tx)} \\ & = \frac{\exp(\beta_{k0}+\beta_k^Tx)}{\sum_{l=0}^{K-1}\exp(\beta_{l0}+\beta_l^Tx)} \\ \text{Pr}(G=K|X=x) &= \frac{\exp(0)}{\sum_{l=0}^{K-1}\exp(\beta_{l0}+\beta_l^Tx)} \end{aligned}and they clearly sum to one.
When $K=2$, this model is especially simple, since there is only a single linear function.
Logistic regression models are usually fit by maximum likelihood, using the conditional likelihood of $G$ given $X$. Since $\text{Pr}(G|X)$ completely specifies the conditional distribution, the multinomial distribution is appropriate.
The log-likelihood for $N$ observation is
\begin{equation} l(\theta) = \sum_{i=1}^N \log p_{g_i}(x_i;\theta), \end{equation}where $p_k(x_i;\theta) = \text{Pr}(G=k|X=x_i;\theta)$
We discuss in detail the two-class case, sine the algorithms simplify considerably. It is convenient to code the two-class $g_i$ via a $0/1$ response $y_i$, where $y_i=1$ when $g_i=1$, and $0$ otherwise. Then we can let
\begin{aligned} p_1(x;\theta) &= p(x;\theta) , \\ p_2(x;\theta) &= 1- p(x;\theta). \\ \end{aligned}And it is easy to show for two-class case, we have
$$ \frac{p(x_i;\beta)}{1-p(x_i;\beta)} = \beta^Tx_i$$The log-likelihood can be written
\begin{aligned} l(\beta) &= \sum_{i=1}^N \left\lbrace y_i\log p(x_i;\beta) + (1-y_i)\log(1-p(x_i;\beta)) \right\rbrace \\ & = \sum_{i=1}^N \left\lbrace y_i [\log p(x_i;\beta) - \log(1-p(x_i;\beta)] + \log(1-p(x_i;\beta)) \right\rbrace \\ & = \sum_{i=1}^N \left\lbrace y_i \log \frac{p(x_i;\beta)}{1-p(x_i;\beta)} + \log(1-p(x_i;\beta)) \right\rbrace \\ &= \sum_{i=1}^N \left\lbrace y_i\beta^Tx_i - \log(1+\exp(\beta^Tx)) \right\rbrace, \end{aligned}where $\beta^T = \lbrace \beta_{10}, \beta_1^T \rbrace$, and we assume that the vector of inputs $x_i$ includes the constant term 1 to acommodate the intercept.
To maximize the log-likelihood, we set its derivatives to zero. These score equations are
$$ \frac{\partial l(\beta)}{\partial\beta} = \sum_{i=1}^N x_i(y_i-p(x_i;\beta)) = 0, $$which are $p+1$ equations nonlinear in $\beta$. Notice that since $x_{i1} =1$, the first score equation specifies that
$$ \sum_{i=1}^N y_i = \sum_{i=1}^N p(x_i;\beta), $$implying that the expected number of class ones matches the observed number (and hence also class twos).
Tips
To solve the score equation, we use the Newton-Raphson algorithm, which requires the second-derivative or Hessian matrix
\begin{equation} \frac{\partial^2 l(\beta)}{\partial\beta\partial\beta^T} = -\sum_{i=1}^N x_ix_i^T p(x_i;\beta)(1-p(x_i;\beta)). \end{equation}Starting with $\beta^{\text{old}}$, a single Newton update is
\begin{equation} \beta^{\text{new}} = \beta^{\text{old}} - \left( \frac{\partial^2 l(\beta)}{\partial\beta\partial\beta^T} \right)^{-1} \frac{\partial l(\beta)}{\partial\beta}, \end{equation}where the derivatives are evaluated at $\beta^{\text{old}}$.
Let
Then we have
\begin{aligned} \frac{\partial l(\beta)}{\partial\beta} &= \mathbf{X}^T(\mathbf{y}-\mathbf{p}) \\ \frac{\partial^2l(\beta)}{\partial\beta\partial\beta^T} &= -\mathbf{X}^T\mathbf{WX}, \end{aligned}and thus the Newton step is
\begin{aligned} \beta^{\text{new}} &= \beta^{\text{old}} + (\mathbf{X}^T\mathbf{WX})^{-1}\mathbf{X}^T(\mathbf{y}-\mathbf{p}) \\ &= (\mathbf{X}^T\mathbf{WX})^{-1} \mathbf{X}^T\mathbf{W}\left( \mathbf{X}\beta^{\text{old}} + \mathbf{W}^{-1}(\mathbf{y}-\mathbf{p}) \right) \\ &= (\mathbf{X}^T\mathbf{WX})^{-1}\mathbf{X}^T\mathbf{W}\mathbf{z}, \end{aligned}where we have re-expressed the Newton step as weighted least squares step, with the response
$$ \mathbf{z} = \mathbf{X}\beta^{\text{old}} + \mathbf{W}^{-1}(\mathbf{y}-\mathbf{p}), $$sometimes known as the adjusted response.
These equations for the Newton step get solved repeatedly, since at each iteration $p$ changes, and hence so does $\mathbf{W}$ and $\mathbf{z}$. This algorithm is referred to as iteratively reweighted least squares or IRLS, since each iteration solves the weighted least squares problem:
$$ \beta^{\text{new}} \leftarrow \arg\min_\beta (\mathbf{z}-\mathbf{X}\beta)^T\mathbf{W}(\mathbf{z}-\mathbf{X}\beta) $$It seems that $\beta=0$ is a good starting value, although convergence is never guaranteed. Typically the algorithm does converge, since the log-likelihood is concave, but overshooting can occur. In the rare cases that the log-likelihood decreases, step size halving will guarantee convergence.
Use the sigmoid function we have:
$$p(x; \beta) = \sigma(z) = \frac{e^z}{1+e^z} = \frac{1}{1+ \exp(-z)}$$where
$$ z = X\beta := w\cdot x + b$$The derivative of the sigmoid is very elegant:
$$\frac{d \sigma }{d z } = \sigma(z) [1- \sigma(z)]$$Then, we have
\begin{aligned} \frac{d p}{d \beta} & = \frac{d \sigma}{d z} \frac{d z}{d \beta} \\ & = \sigma(z) [1- \sigma(z)] X^T \\ & = p(x; \beta)[1 - p(x; \beta)] X^T \end{aligned}For the following equation,
$$ \frac{\partial l(\beta)}{\partial\beta} = \sum_{i=1}^N x_i(y_i-p(x_i;\beta)) $$Its second derivative is easy to derive now:
$$ \frac{\partial^2 l(\beta)}{\partial\beta\partial\beta^T} = -\sum_{i=1}^N x_ix_i^T p(x_i;\beta)(1-p(x_i;\beta)). $$Tips
The neural network uses sigmoid and softmax functions a lot. Moreover, the loss function is just the negativity of log-likelihood function. Therefore, we will go through those derivations.
The first derivative takes a long time and has more equations. Nevertheless, we could still do it with several components.
For our log-likelihood function
$$ L(\beta) = \sum_{i=1}^N \left\lbrace y_i\log p(x_i;\beta) + (1-y_i)\log(1-p(x_i\beta)) \right\rbrace $$It is easy to have
$$\frac{d L}{d p} = \frac{y}{p} - \frac{1-y}{1-p}$$We have already shown :
$$\frac{d p}{d \beta} = p(x; \beta)[1 - p(x; \beta)] X^T = p(1 - p)X^T$$Now, let's put them together
\begin{aligned} \frac{dL}{d \beta} & = \frac{d L}{d p} \frac{dp}{d \beta} \\ & = \big [ \frac{y}{p} - \frac{1-y}{1-p} \big ] [p(1 - p)X^T] \\ & = \frac{y-p}{p(1-p)}[p(1 - p)X^T] \\ & = (y-p)X^T \end{aligned}which is equivalent to
$$ \frac{\partial l(\beta)}{\partial\beta} = \sum_{i=1}^N x_i(y_i-p(x_i;\beta)) $$Tips
Since p, 1-p and p(1-p) are scalar, that's why we have to take the diagnonal element when we implement the matrix computation.
# implement a simple logistic regression for binary case
# the close form of solution
def sigmoid(x):
# sigmoid function
return 1/(1+np.exp(-x))
def gradient(x, y, beta):
"""
The first derivative of log-likelihood function
Based on equation (4.24 or 4.21)
x: n by p+1 matrix (with constant)
y: n by 1 vector
beta: p+1 by 1 vector
Return [(p+1) by 1 row vector]
"""
z = x @ beta # n by 1 vector
phat = sigmoid(z) # n by 1 vector
return x.T @ (y - phat)
def hessian(x, beta):
"""
The second derivative of log-likelihood function
Based on equation (4.25 or 4.23)
x: n by p+1 matrix
beta: parameters, p+1 by 1
Return: p+1 by p+1 matrix
"""
z = x @ beta # n by 1 vector
phat = sigmoid(z) # n by 1 vector
# flatten the phat vector
# ! Important step
phat = phat.flatten()
# create the diagnoal matrix filled with 0s
w = np.diag(phat*(1-phat)) # n by n matrix
return - x.T @ w @ x
def newton(x, y, beta_0, G, H, epsilon, max_iter):
"""
Newton's method to estimate parameters
beta_0: initial values p+1 by 1
epsilon: convergence rate
G: gradient function
H: hessian function
"""
# !Important to copy, otherwise all values will be changed
beta = beta_0.copy()
# initialize the different of beta_old and new
delta = 1 # shoul be positive
iteration = 0
while delta > epsilon and iteration < max_iter:
# save the orginal value before updating
beta_old = beta.copy()
# update beta, [p+1, p+1] @ [p+1, 1]
beta -= np.linalg.inv(H(x, beta)) @ G(x, y, beta)
iteration += 1
# calculate the standard error
# std err is sqrt of diagonal of inverse of negative hessian
neg_hessian = -H(x, beta)
neg_hessian_inv = np.linalg.inv(neg_hessian)
std_err = np.sqrt(np.diag(neg_hessian_inv))
# one could also estimate the standard error by
# doing boostrapping (100 estimation with different samples)
return beta, std_err
Tips
Later we will just use loss function and gradient descent method to estimate coefficients, which will use more iterations as it is dealing with the first order derivative.
Here we present an analysis of binary data to illustrate the traditional statistical use of the logistic regression model.
# read heart disease data
sa_heart = pd.read_csv('./data/heart/SAheart.data', index_col=0)
sa_heart.head()
| sbp | tobacco | ldl | adiposity | famhist | typea | obesity | alcohol | age | chd | |
|---|---|---|---|---|---|---|---|---|---|---|
| row.names | ||||||||||
| 1 | 160 | 12.00 | 5.73 | 23.11 | Present | 49 | 25.30 | 97.20 | 52 | 1 |
| 2 | 144 | 0.01 | 4.41 | 28.61 | Absent | 55 | 28.87 | 2.06 | 63 | 1 |
| 3 | 118 | 0.08 | 3.48 | 32.28 | Present | 52 | 29.14 | 3.81 | 46 | 0 |
| 4 | 170 | 7.50 | 6.41 | 38.03 | Present | 51 | 31.99 | 24.26 | 58 | 1 |
| 5 | 134 | 13.60 | 3.50 | 27.78 | Present | 60 | 25.99 | 57.34 | 49 | 1 |
# we will only use four variables
sa_heart.pop('adiposity')
sa_heart.pop('typea')
# creat dummy for famhist
sa_heart['famhist'] = sa_heart['famhist'].map(
{
'Present': 1, 'Absent': 0
}
)
sa_heart.head()
| sbp | tobacco | ldl | famhist | obesity | alcohol | age | chd | |
|---|---|---|---|---|---|---|---|---|
| row.names | ||||||||
| 1 | 160 | 12.00 | 5.73 | 1 | 25.30 | 97.20 | 52 | 1 |
| 2 | 144 | 0.01 | 4.41 | 0 | 28.87 | 2.06 | 63 | 1 |
| 3 | 118 | 0.08 | 3.48 | 1 | 29.14 | 3.81 | 46 | 0 |
| 4 | 170 | 7.50 | 6.41 | 1 | 31.99 | 24.26 | 58 | 1 |
| 5 | 134 | 13.60 | 3.50 | 1 | 25.99 | 57.34 | 49 | 1 |
# prepare x and y
sa_df_y = sa_heart.pop('chd')
sa_y = sa_df_y.values.reshape(-1, 1)
sa_x = sa_heart.values
# plot the grapha
colors = sa_df_y.apply(lambda y: 'C1' if y else 'C0')
pd.plotting.scatter_matrix(sa_heart, color=colors, figsize=(10, 10));
# fit logistic model
n, p = sa_x.shape
x_const = np.hstack([np.ones((n, 1)), sa_x])
beta_initial = np.zeros((p+1, 1))
beta_est, std_errors = newton(
x_const, sa_y, beta_initial, gradient, hessian,
1e-6, 100
)
print('{0:>15} {1:>15} {2:>15} {3:>15}'.format('Term', 'Coefficient',
'Std. Error', 'Z Score'))
print('-'*64)
table_term = ['intercept'] + list(sa_heart.columns)
for term, coeff, std_err in zip(table_term, beta_est, std_errors):
print('{0:>15} {1:>15.3f} {2:>15.3f} {3:>15.3f}'.format(
term, float(coeff), float(std_err),
float(coeff)/float(std_err)
))
Term Coefficient Std. Error Z Score
----------------------------------------------------------------
intercept -4.130 0.964 -4.283
sbp 0.006 0.006 1.023
tobacco 0.080 0.026 3.034
ldl 0.185 0.057 3.218
famhist 0.939 0.225 4.177
obesity -0.035 0.029 -1.187
alcohol 0.001 0.004 0.136
age 0.043 0.010 4.181
When we calculate the second derivate, we could get the Fisher informtion
$$I(\beta) = - E [\frac{\partial^2l(\beta)}{\partial\beta\partial\beta^T}]= E[\mathbf{X}^T\mathbf{WX}]$$The approximate sample distribution of $\hat{\beta}$ for large $n$ is
$$N[\beta, (X^TWX)^{-1}]$$How does one interpret $\textsf{tobacco}$ coefficient of $0.081$ ($\text{Std. Error} = 0.026$), for example?
An increase of $1\text{kg}$ in lifetime tobacco usage accounts for an increase in the odds of coronary heart disease of $\exp(0.081)=1.084$ or $8.4\%$.
Incorporating the standard error we get an approximate $95\%$ confidence interval of
$$ \exp(0.081 \pm 2\times 0.026) = (1.03, 1.14). $$We see that some of the variables have nonlinear effects, and when modeled appropriately, are not excluded from the model.
It is generally felt that logistic regression is a safer, more robust bet than the LDA model, relying on fewer assumptions. It is our experience that the models give very similar results, even when LDA is used inappropriately, such as with qualitative predictors.
LDA could be also used as a dimension reduction tool.